Easy Way to Detect Victoryu Java Tic Tac Toe
Prerequisites: Minimax Algorithm in Game Theory, Evaluation Function in Game Theory
Let us combine what we have learnt so far about minimax and evaluation function to write a proper Tic-Tac-Toe AI (Artificial Intelligence) that plays a perfect game. This AI will consider all possible scenarios and makes the most optimal move.
Finding the Best Move :
We shall be introducing a new function called findBestMove(). This function evaluates all the available moves using minimax() and then returns the best move the maximizer can make. The pseudocode is as follows :
function findBestMove(board): bestMove = NULL for each move in board : if current move is better than bestMove bestMove = current move return bestMove
Minimax :
To check whether or not the current move is better than the best move we take the help of minimax() function which will consider all the possible ways the game can go and returns the best value for that move, assuming the opponent also plays optimally
The code for the maximizer and minimizer in the minimax() function is similar to findBestMove(), the only difference is, instead of returning a move, it will return a value. Here is the pseudocode :
function minimax(board, depth, isMaximizingPlayer): if current board state is a terminal state : return value of the board if isMaximizingPlayer : bestVal = -INFINITY for each move in board : value = minimax(board, depth+1, false) bestVal = max( bestVal, value) return bestVal else : bestVal = +INFINITY for each move in board : value = minimax(board, depth+1, true) bestVal = min( bestVal, value) return bestVal
Checking for GameOver state :
To check whether the game is over and to make sure there are no moves left we use isMovesLeft() function. It is a simple straightforward function which checks whether a move is available or not and returns true or false respectively. Pseudocode is as follows :
function isMovesLeft(board): for each cell in board: if current cell is empty: return true return false
Making our AI smarter :
One final step is to make our AI a little bit smarter. Even though the following AI plays perfectly, it might choose to make a move which will result in a slower victory or a faster loss. Lets take an example and explain it.
Assume that there are 2 possible ways for X to win the game from a give board state.
- Move A : X can win in 2 move
- Move B : X can win in 4 moves
Our evaluation function will return a value of +10 for both moves A and B . Even though the move A is better because it ensures a faster victory, our AI may choose B sometimes. To overcome this problem we subtract the depth value from the evaluated score. This means that in case of a victory it will choose a the victory which takes least number of moves and in case of a loss it will try to prolong the game and play as many moves as possible. So the new evaluated value will be
- Move A will have a value of +10 – 2 = 8
- Move B will have a value of +10 – 4 = 6
Now since move A has a higher score compared to move B our AI will choose move A over move B . The same thing must be applied to the minimizer. Instead of subtracting the depth we add the depth value as the minimizer always tries to get, as negative a value as possible. We can subtract the depth either inside the evaluation function or outside it. Anywhere is fine. I have chosen to do it outside the function. Pseudocode implementation is as follows.
if maximizer has won: return WIN_SCORE – depth else if minimizer has won: return LOOSE_SCORE + depth
Below is implementation of above idea.
C++
#include<bits/stdc++.h>
using namespace std;
struct Move
{
int row, col;
};
char player = 'x' , opponent = 'o' ;
bool isMovesLeft( char board[3][3])
{
for ( int i = 0; i<3; i++)
for ( int j = 0; j<3; j++)
if (board[i][j]== '_' )
return true ;
return false ;
}
int evaluate( char b[3][3])
{
for ( int row = 0; row<3; row++)
{
if (b[row][0]==b[row][1] &&
b[row][1]==b[row][2])
{
if (b[row][0]==player)
return +10;
else if (b[row][0]==opponent)
return -10;
}
}
for ( int col = 0; col<3; col++)
{
if (b[0][col]==b[1][col] &&
b[1][col]==b[2][col])
{
if (b[0][col]==player)
return +10;
else if (b[0][col]==opponent)
return -10;
}
}
if (b[0][0]==b[1][1] && b[1][1]==b[2][2])
{
if (b[0][0]==player)
return +10;
else if (b[0][0]==opponent)
return -10;
}
if (b[0][2]==b[1][1] && b[1][1]==b[2][0])
{
if (b[0][2]==player)
return +10;
else if (b[0][2]==opponent)
return -10;
}
return 0;
}
int minimax( char board[3][3], int depth, bool isMax)
{
int score = evaluate(board);
if (score == 10)
return score;
if (score == -10)
return score;
if (isMovesLeft(board)== false )
return 0;
if (isMax)
{
int best = -1000;
for ( int i = 0; i<3; i++)
{
for ( int j = 0; j<3; j++)
{
if (board[i][j]== '_' )
{
board[i][j] = player;
best = max( best,
minimax(board, depth+1, !isMax) );
board[i][j] = '_' ;
}
}
}
return best;
}
else
{
int best = 1000;
for ( int i = 0; i<3; i++)
{
for ( int j = 0; j<3; j++)
{
if (board[i][j]== '_' )
{
board[i][j] = opponent;
best = min(best,
minimax(board, depth+1, !isMax));
board[i][j] = '_' ;
}
}
}
return best;
}
}
Move findBestMove( char board[3][3])
{
int bestVal = -1000;
Move bestMove;
bestMove.row = -1;
bestMove.col = -1;
for ( int i = 0; i<3; i++)
{
for ( int j = 0; j<3; j++)
{
if (board[i][j]== '_' )
{
board[i][j] = player;
int moveVal = minimax(board, 0, false );
board[i][j] = '_' ;
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
printf ( "The value of the best Move is : %d\n\n" ,
bestVal);
return bestMove;
}
int main()
{
char board[3][3] =
{
{ 'x' , 'o' , 'x' },
{ 'o' , 'o' , 'x' },
{ '_' , '_' , '_' }
};
Move bestMove = findBestMove(board);
printf ( "The Optimal Move is :\n" );
printf ( "ROW: %d COL: %d\n\n" , bestMove.row,
bestMove.col );
return 0;
}
Java
class GFG
{
static class Move
{
int row, col;
};
static char player = 'x' , opponent = 'o' ;
static Boolean isMovesLeft( char board[][])
{
for ( int i = 0 ; i < 3 ; i++)
for ( int j = 0 ; j < 3 ; j++)
if (board[i][j] == '_' )
return true ;
return false ;
}
static int evaluate( char b[][])
{
for ( int row = 0 ; row < 3 ; row++)
{
if (b[row][ 0 ] == b[row][ 1 ] &&
b[row][ 1 ] == b[row][ 2 ])
{
if (b[row][ 0 ] == player)
return + 10 ;
else if (b[row][ 0 ] == opponent)
return - 10 ;
}
}
for ( int col = 0 ; col < 3 ; col++)
{
if (b[ 0 ][col] == b[ 1 ][col] &&
b[ 1 ][col] == b[ 2 ][col])
{
if (b[ 0 ][col] == player)
return + 10 ;
else if (b[ 0 ][col] == opponent)
return - 10 ;
}
}
if (b[ 0 ][ 0 ] == b[ 1 ][ 1 ] && b[ 1 ][ 1 ] == b[ 2 ][ 2 ])
{
if (b[ 0 ][ 0 ] == player)
return + 10 ;
else if (b[ 0 ][ 0 ] == opponent)
return - 10 ;
}
if (b[ 0 ][ 2 ] == b[ 1 ][ 1 ] && b[ 1 ][ 1 ] == b[ 2 ][ 0 ])
{
if (b[ 0 ][ 2 ] == player)
return + 10 ;
else if (b[ 0 ][ 2 ] == opponent)
return - 10 ;
}
return 0 ;
}
static int minimax( char board[][],
int depth, Boolean isMax)
{
int score = evaluate(board);
if (score == 10 )
return score;
if (score == - 10 )
return score;
if (isMovesLeft(board) == false )
return 0 ;
if (isMax)
{
int best = - 1000 ;
for ( int i = 0 ; i < 3 ; i++)
{
for ( int j = 0 ; j < 3 ; j++)
{
if (board[i][j]== '_' )
{
board[i][j] = player;
best = Math.max(best, minimax(board,
depth + 1 , !isMax));
board[i][j] = '_' ;
}
}
}
return best;
}
else
{
int best = 1000 ;
for ( int i = 0 ; i < 3 ; i++)
{
for ( int j = 0 ; j < 3 ; j++)
{
if (board[i][j] == '_' )
{
board[i][j] = opponent;
best = Math.min(best, minimax(board,
depth + 1 , !isMax));
board[i][j] = '_' ;
}
}
}
return best;
}
}
static Move findBestMove( char board[][])
{
int bestVal = - 1000 ;
Move bestMove = new Move();
bestMove.row = - 1 ;
bestMove.col = - 1 ;
for ( int i = 0 ; i < 3 ; i++)
{
for ( int j = 0 ; j < 3 ; j++)
{
if (board[i][j] == '_' )
{
board[i][j] = player;
int moveVal = minimax(board, 0 , false );
board[i][j] = '_' ;
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
System.out.printf( "The value of the best Move " +
"is : %d\n\n" , bestVal);
return bestMove;
}
public static void main(String[] args)
{
char board[][] = {{ 'x' , 'o' , 'x' },
{ 'o' , 'o' , 'x' },
{ '_' , '_' , '_' }};
Move bestMove = findBestMove(board);
System.out.printf( "The Optimal Move is :\n" );
System.out.printf( "ROW: %d COL: %d\n\n" ,
bestMove.row, bestMove.col );
}
}
Python3
player, opponent = 'x' , 'o'
def isMovesLeft(board) :
for i in range ( 3 ) :
for j in range ( 3 ) :
if (board[i][j] = = '_' ) :
return True
return False
def evaluate(b) :
for row in range ( 3 ) :
if (b[row][ 0 ] = = b[row][ 1 ] and b[row][ 1 ] = = b[row][ 2 ]) :
if (b[row][ 0 ] = = player) :
return 10
elif (b[row][ 0 ] = = opponent) :
return - 10
for col in range ( 3 ) :
if (b[ 0 ][col] = = b[ 1 ][col] and b[ 1 ][col] = = b[ 2 ][col]) :
if (b[ 0 ][col] = = player) :
return 10
elif (b[ 0 ][col] = = opponent) :
return - 10
if (b[ 0 ][ 0 ] = = b[ 1 ][ 1 ] and b[ 1 ][ 1 ] = = b[ 2 ][ 2 ]) :
if (b[ 0 ][ 0 ] = = player) :
return 10
elif (b[ 0 ][ 0 ] = = opponent) :
return - 10
if (b[ 0 ][ 2 ] = = b[ 1 ][ 1 ] and b[ 1 ][ 1 ] = = b[ 2 ][ 0 ]) :
if (b[ 0 ][ 2 ] = = player) :
return 10
elif (b[ 0 ][ 2 ] = = opponent) :
return - 10
return 0
def minimax(board, depth, isMax) :
score = evaluate(board)
if (score = = 10 ) :
return score
if (score = = - 10 ) :
return score
if (isMovesLeft(board) = = False ) :
return 0
if (isMax) :
best = - 1000
for i in range ( 3 ) :
for j in range ( 3 ) :
if (board[i][j] = = '_' ) :
board[i][j] = player
best = max ( best, minimax(board,
depth + 1 ,
not isMax) )
board[i][j] = '_'
return best
else :
best = 1000
for i in range ( 3 ) :
for j in range ( 3 ) :
if (board[i][j] = = '_' ) :
board[i][j] = opponent
best = min (best, minimax(board, depth + 1 , not isMax))
board[i][j] = '_'
return best
def findBestMove(board) :
bestVal = - 1000
bestMove = ( - 1 , - 1 )
for i in range ( 3 ) :
for j in range ( 3 ) :
if (board[i][j] = = '_' ) :
board[i][j] = player
moveVal = minimax(board, 0 , False )
board[i][j] = '_'
if (moveVal > bestVal) :
bestMove = (i, j)
bestVal = moveVal
print ( "The value of the best Move is :" , bestVal)
print ()
return bestMove
board = [
[ 'x' , 'o' , 'x' ],
[ 'o' , 'o' , 'x' ],
[ '_' , '_' , '_' ]
]
bestMove = findBestMove(board)
print ( "The Optimal Move is :" )
print ( "ROW:" , bestMove[ 0 ], " COL:" , bestMove[ 1 ])
C#
using System;
using System.Collections.Generic;
class GFG
{
class Move
{
public int row, col;
};
static char player = 'x' , opponent = 'o' ;
static Boolean isMovesLeft( char [,]board)
{
for ( int i = 0; i < 3; i++)
for ( int j = 0; j < 3; j++)
if (board[i, j] == '_' )
return true ;
return false ;
}
static int evaluate( char [,]b)
{
for ( int row = 0; row < 3; row++)
{
if (b[row, 0] == b[row, 1] &&
b[row, 1] == b[row, 2])
{
if (b[row, 0] == player)
return +10;
else if (b[row, 0] == opponent)
return -10;
}
}
for ( int col = 0; col < 3; col++)
{
if (b[0, col] == b[1, col] &&
b[1, col] == b[2, col])
{
if (b[0, col] == player)
return +10;
else if (b[0, col] == opponent)
return -10;
}
}
if (b[0, 0] == b[1, 1] && b[1, 1] == b[2, 2])
{
if (b[0, 0] == player)
return +10;
else if (b[0, 0] == opponent)
return -10;
}
if (b[0, 2] == b[1, 1] && b[1, 1] == b[2, 0])
{
if (b[0, 2] == player)
return +10;
else if (b[0, 2] == opponent)
return -10;
}
return 0;
}
static int minimax( char [,]board,
int depth, Boolean isMax)
{
int score = evaluate(board);
if (score == 10)
return score;
if (score == -10)
return score;
if (isMovesLeft(board) == false )
return 0;
if (isMax)
{
int best = -1000;
for ( int i = 0; i < 3; i++)
{
for ( int j = 0; j < 3; j++)
{
if (board[i, j] == '_' )
{
board[i, j] = player;
best = Math.Max(best, minimax(board,
depth + 1, !isMax));
board[i, j] = '_' ;
}
}
}
return best;
}
else
{
int best = 1000;
for ( int i = 0; i < 3; i++)
{
for ( int j = 0; j < 3; j++)
{
if (board[i, j] == '_' )
{
board[i, j] = opponent;
best = Math.Min(best, minimax(board,
depth + 1, !isMax));
board[i, j] = '_' ;
}
}
}
return best;
}
}
static Move findBestMove( char [,]board)
{
int bestVal = -1000;
Move bestMove = new Move();
bestMove.row = -1;
bestMove.col = -1;
for ( int i = 0; i < 3; i++)
{
for ( int j = 0; j < 3; j++)
{
if (board[i, j] == '_' )
{
board[i, j] = player;
int moveVal = minimax(board, 0, false );
board[i, j] = '_' ;
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
Console.Write( "The value of the best Move " +
"is : {0}\n\n" , bestVal);
return bestMove;
}
public static void Main(String[] args)
{
char [,]board = {{ 'x' , 'o' , 'x' },
{ 'o' , 'o' , 'x' },
{ '_' , '_' , '_' }};
Move bestMove = findBestMove(board);
Console.Write( "The Optimal Move is :\n" );
Console.Write( "ROW: {0} COL: {1}\n\n" ,
bestMove.row, bestMove.col );
}
}
Javascript
<script>
class Move
{
constructor()
{
let row,col;
}
}
let player = 'x' , opponent = 'o' ;
function isMovesLeft(board)
{
for (let i = 0; i < 3; i++)
for (let j = 0; j < 3; j++)
if (board[i][j] == '_' )
return true ;
return false ;
}
function evaluate(b)
{
for (let row = 0; row < 3; row++)
{
if (b[row][0] == b[row][1] &&
b[row][1] == b[row][2])
{
if (b[row][0] == player)
return +10;
else if (b[row][0] == opponent)
return -10;
}
}
for (let col = 0; col < 3; col++)
{
if (b[0][col] == b[1][col] &&
b[1][col] == b[2][col])
{
if (b[0][col] == player)
return +10;
else if (b[0][col] == opponent)
return -10;
}
}
if (b[0][0] == b[1][1] && b[1][1] == b[2][2])
{
if (b[0][0] == player)
return +10;
else if (b[0][0] == opponent)
return -10;
}
if (b[0][2] == b[1][1] &&
b[1][1] == b[2][0])
{
if (b[0][2] == player)
return +10;
else if (b[0][2] == opponent)
return -10;
}
return 0;
}
function minimax(board, depth, isMax)
{
let score = evaluate(board);
if (score == 10)
return score;
if (score == -10)
return score;
if (isMovesLeft(board) == false )
return 0;
if (isMax)
{
let best = -1000;
for (let i = 0; i < 3; i++)
{
for (let j = 0; j < 3; j++)
{
if (board[i][j]=='_ ')
{
// Make the move
board[i][j] = player;
// Call minimax recursively
// and choose the maximum value
best = Math.max(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i][j] = ' _ ';
}
}
}
return best;
}
// If this minimizer' s move
else
{
let best = 1000;
for (let i = 0; i < 3; i++)
{
for (let j = 0; j < 3; j++)
{
if (board[i][j] == '_' )
{
board[i][j] = opponent;
best = Math.min(best, minimax(board,
depth + 1, !isMax));
board[i][j] = '_' ;
}
}
}
return best;
}
}
function findBestMove(board)
{
let bestVal = -1000;
let bestMove = new Move();
bestMove.row = -1;
bestMove.col = -1;
for (let i = 0; i < 3; i++)
{
for (let j = 0; j < 3; j++)
{
if (board[i][j] == '_' )
{
board[i][j] = player;
let moveVal = minimax(board, 0, false );
board[i][j] = '_' ;
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
document.write( "The value of the best Move " +
"is : " , bestVal + "<br><br>" );
return bestMove;
}
let board = [ [ 'x' , 'o' , 'x' ],
[ 'o' , 'o' , 'x' ],
[ '_' , '_' , '_' ] ];
let bestMove = findBestMove(board);
document.write( "The Optimal Move is :<br>" );
document.write( "ROW: " + bestMove.row +
" COL: " + bestMove.col + "<br>" );
</script>
Output :
The value of the best Move is : 10 The Optimal Move is : ROW: 2 COL: 2
Explanation :
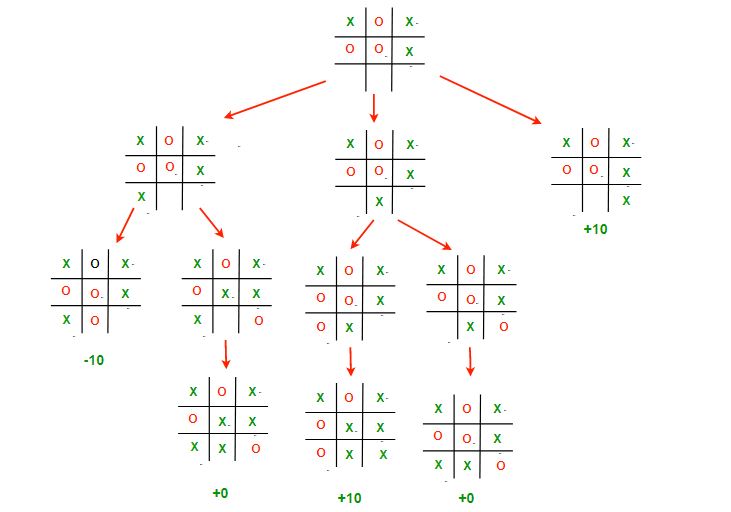
This image depicts all the possible paths that the game can take from the root board state. It is often called the Game Tree.
The 3 possible scenarios in the above example are :
- Left Move : If X plays [2,0]. Then O will play [2,1] and win the game. The value of this move is -10
- Middle Move : If X plays [2,1]. Then O will play [2,2] which draws the game. The value of this move is 0
- Right Move : If X plays [2,2]. Then he will win the game. The value of this move is +10;
Remember, even though X has a possibility of winning if he plays the middle move, O will never let that happen and will choose to draw instead.
Therefore the best choice for X, is to play [2,2], which will guarantee a victory for him.
We do encourage our readers to try giving various inputs and understanding why the AI choose to play that move. Minimax may confuse programmers as it it thinks several moves in advance and is very hard to debug at times. Remember this implementation of minimax algorithm can be applied any 2 player board game with some minor changes to the board structure and how we iterate through the moves. Also sometimes it is impossible for minimax to compute every possible game state for complex games like Chess. Hence we only compute upto a certain depth and use the evaluation function to calculate the value of the board.
Stay tuned for next weeks article where we shall be discussing about Alpha-Beta pruning that can drastically improve the time taken by minimax to traverse a game tree.
This article is contributed by Akshay L Aradhya. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Source: https://www.geeksforgeeks.org/minimax-algorithm-in-game-theory-set-3-tic-tac-toe-ai-finding-optimal-move/
0 Response to "Easy Way to Detect Victoryu Java Tic Tac Toe"
Post a Comment